Ahh, no I don't think so.
It was more like a replacement for finding a "common denominator" when dealing with a fraction.
Instead, they follow a rote process of multiplying out - depending on what you're doing with the fractions (adding or dividing or whatever) - they "cross multiply".
Just an example:
Say you need to add 2/3 + 1/2.
I would find a "common denominator" so the two fractions can be worked together:
2/3 = 4/6 and 1/2=3/6. Now you can add them. Or subtract them. And you're getting a feel for how the compare, etc.
4/6 + 3/6 = 7/6 and you can then reduce that to 1 1/6.
They were taught instead, to "cross multiply".
You multiply the 2x2 and the 1x3 (why? Because the teacher says so).
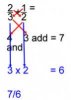
So literally,
they were being taught to move numbers around in a particular way ("cross multiply")
to solve a particular type of problem (adding fractions with different denominators) INSTEAD of being taught to really understand the concept of it, which would let them THINK about fractional amounts and enable them to work with them, even with different challenges (like dividing them, or converting them to decimal, etc).
You get the answer, but you don't learn anything that'll last. Super.
A teacher could
USE this method - if they were explaining WHY it works. But that's not in the curriculum as far as I could tell.
Or maybe it is, but our teachers skipped that part.
So if they are making kids figure out: 16 + 17 = ?
Instead of:
16
+17
_____
1
16
+17
____
3
1
16
+17
____
33. Like we all were taught, they are getting:
16
+17
_____
10
10
6
+7
____
10
10
+13
_____
10
10
+13
____
33
Is that it?






